
Dans les rubriques « Division CE2 » et « Division CM1 – CM2 » , découvrez un ensemble de ressources pédagogiques sur les divisions posées avec un nombre entier à deux chiffres au diviseur. Vous trouverez dans un premier temps une série de fiches d’exercices sur la division posée à deux chiffres pour le CE2 – CM1 – CM2 à imprimer en PDF. Plus bas dans la page, nous proposons également une leçon avec des explications complètes pour apprendre à poser une division à deux chiffres. Au préalable, nous vous recommandons de consulter notre leçon et nos exercices sur la division posée à un chiffre.

Récréakidz met à votre disposition 4 fiches d’exercices sur la division posée à 2 chiffres (niveau CE2 – CM1 – CM2) à imprimer gratuitement au format PDF.
Dans ces fiches (accompagnées de la correction), nous demandons à l’élève :

Voici les 3 éléments qui constituent une division posée en colonne :
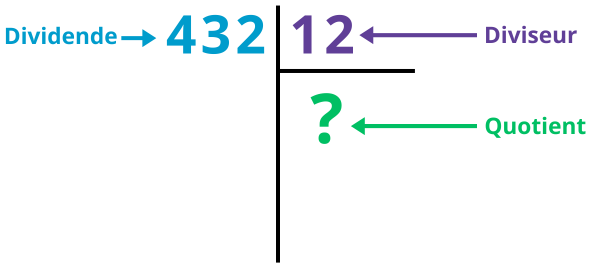
Ici, je pose la division 432 : 12.
Voici les emplacements des 3 éléments qui constituent une division posée en colonne :
Pour résoudre une division posée en colonne à deux chiffres, je cherche par quel nombre je dois multiplier le diviseur pour trouver un nombre entier égal ou proche du dividende sans le dépasser.
Je vais donc procéder étape par étape en cherchant par quel nombre je dois multiplier le diviseur pour trouver un nombre entier égale ou proche de chaque chiffre du dividende (sans le dépasser), en commençant toujours par les deux premiers chiffres à gauche.
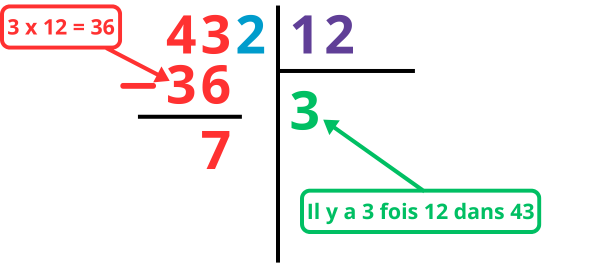
Étape 1 : je commence avec les deux premiers chiffre du dividende, je me pose la question : combien de fois y a-t-il 12 dans 43 ? Car 43 sont les deux premier chiffre du dividende.
Je me rappelle de la table de 12 :
1 x 12 = 12
2 x 12 = 24
3 x 12 = 36
4 x 12 = 48. 48 est trop grand par rapport à 43 donc il y a 3 fois 12 dans 43.
J’écris donc 3 au niveau du quotient et je soustrais 3 x 12 donc 36 aux deux premier chiffres du dividende 432 (donc ici 43).
43 – 36 = 7 donc j’écris 7 sous la barre de la soustraction (dans la colonne des dizaines).
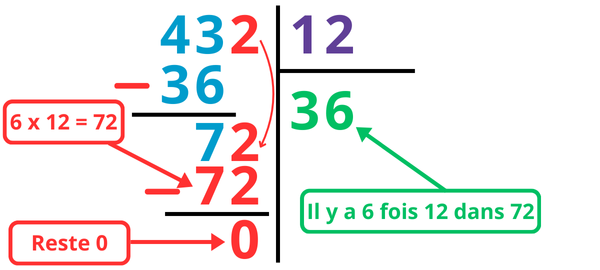
Étape 2 : je descends ensuite le 2 de 432 pour pouvoir continuer ma division.
Pour continuer, on se pose la question : 12 multiplié par combien donne 72 ? ou combien de fois y a-t-il 12 dans 72 ?
Je me rappelle de la table de 12 :
1 x 12 = 12
2 x 12 = 24
3 x 12 = 36
4 x 12 = 48
5 x 12 = 60
6 x 12 = 72 donc il y a 6 fois 12 dans 72.
Je note donc 6 à la suite du 3 au niveau du quotient et je soustrais 6 x 12 donc 72 à mon 72 restant à gauche de la barre verticale.
72 – 72 = 0. J’obtiens 0 donc il n’ y a pas de reste !
Ici, je dois résoudre la division 5 236 : 25.
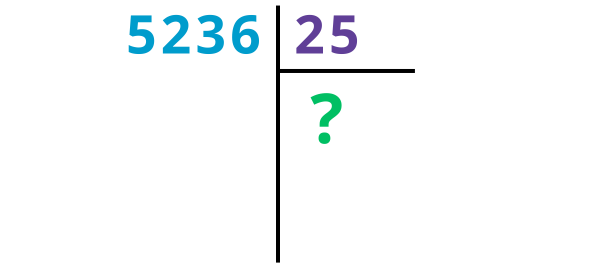
Combien de fois y a-t-il 25 dans 5 236 ?
C’est compliqué à calculer de tête… Je vais donc résoudre la division étape par étape !
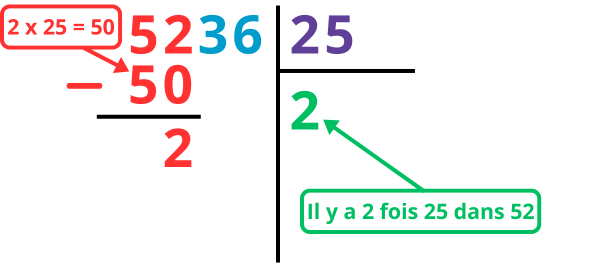
Étape 1 : je commence avec les deux premiers chiffres du dividende, je me pose la question : combien de fois y a-t-il 25 dans 52 ? Car 52 correspond aux deux premiers chiffres du dividende.
Je me rappelle de la table de 25 :
1 x 25 = 25
2 x 25 = 50
3 x 25 = 75. 75 est trop grand par rapport à 52 donc il y a 2 fois 25 dans 52.
J’écris donc 2 au niveau du quotient et je soustrais 2 x 25 donc 50 aux deux premiers chiffres du dividende 5236 (donc ici 52).
52 – 50 = 2 donc j’écris 2 sous la barre de la soustraction (dans la colonne des centaines).
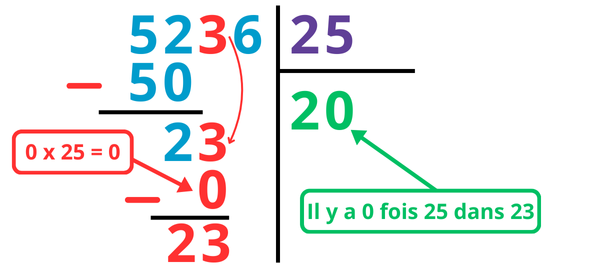
Étape 2 : je descends ensuite le 3 de 5 236 pour pouvoir continuer ma division.
Pour continuer, on se pose la question : 25 multiplié par combien donne 23 ? ou combien de fois y a-t-il 25 dans 23 ?
Je me rappelle de la table de 25 :
1 x 25 = 25. 25 est trop grand par rapport à 23 donc il y a 0 fois 25 dans 23.
Je note donc 0 à la suite du 2 au niveau du quotient et je soustrais 0 x 25 donc 0 à 23 à gauche de la barre verticale.
23 – 0 = 23 donc j’écris 23 sous la barre de la soustraction.
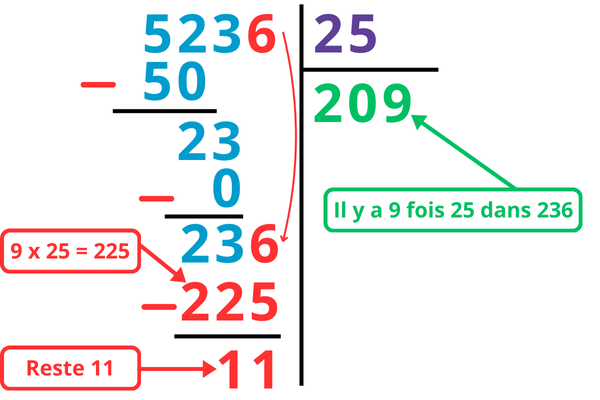
Étape 3 : je descends ensuite le 6 de 5 236 pour pouvoir continuer ma division.
Pour continuer, on se pose la question : 25 multiplié par combien donne 236 ? ou combien de fois y a-t-il 25 dans 236 ?
Je me rappelle de la table de 25 :
1 x 25 = 25
2 x 25 = 50
3 x 25 = 75
4 x 25 = 100
5 x 25 = 125
6 x 25 = 150
7 x 25 = 175
8 x 25 = 200
9 x 25 = 225
10 x 25 = 250. 250 est trop grand par rapport à 236 donc il y a 9 fois 25 dans 236.
Je note donc 9 à la suite du 0 au niveau du quotient et je soustrais 9 x 25 donc 225 à 236 à gauche de la barre verticale.
236 – 225 = 11. J’obtiens 11 donc il reste 11 !