Dans les rubriques « Soustraction CE1 – CE2 » et « Soustraction CM1 – CM2 » , découvrez un ensemble de ressources pédagogiques sur les soustractions posées en colonne avec retenue. Vous trouverez dans un premier temps une série de fiches d’exercices sur la soustraction posée en colonne avec retenue pour le CE1 – CE2 et le CM1 – CM2 à imprimer en PDF. Plus bas dans la page, nous proposons également une leçon avec des explications complètes pour apprendre à faire des soustractions posées en colonne avec retenue (à l’aide de deux méthodes : par cassage ou par conservation des écarts). Pour aller plus loin, découvrez également notre leçon et nos exercices sur la soustraction posée sans retenue et l’addition posée en colonne avec retenue.

Récréakidz met à votre disposition 6 fiches d’exercices sur les soustractions posées en colonne avec retenue (niveau CE1 – CE2 – CM1 – CM2) à imprimer gratuitement au format PDF.
Dans ces fiches (accompagnées de la correction), nous demandons à l’élève :

Ici il s’agit d’une soustraction de nombres à 2 chiffres. Pour poser la soustraction en colonne, je place les unités sous les unités et les dizaines sous les dizaines, puis je soustrais les chiffres de chaque colonne. Ici, il s’agit d’une soustraction posée avec retenue, découvrons ensemble deux méthodes pour la résoudre : la méthode par conservation des écarts et la méthode par cassage.
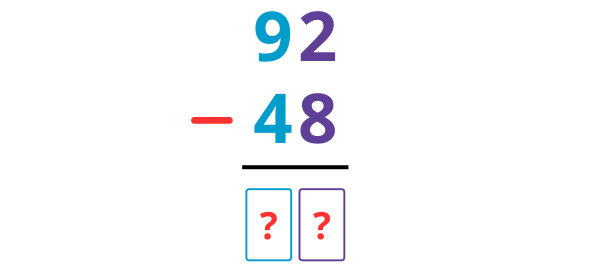
Je commence par les unités : mais calculer 2 – 8 est impossible !
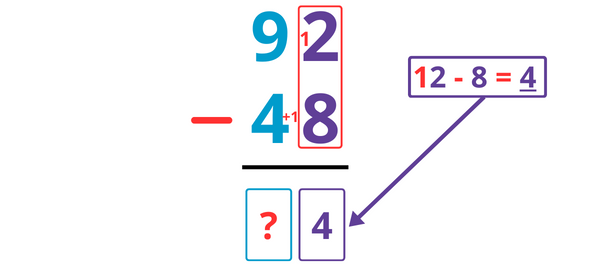
Avant de soustraire les unités, j’emprunte donc une dizaine que j’ajoute au premier terme dans la colonne des unités (ici le chiffre 2 devient donc 12).
12 – 8 = 4, je note donc 4 dans la colonne des unités.
Mais attention, j’ai emprunté une dizaine, il faut la rendre ! J’ajoute donc +1 au deuxième terme dans la colonne des dizaines (ici j’ajoute donc +1 à côté du chiffre 4).
Je soustrais ensuite les dizaines en n’oubliant pas d’ajouter la retenue !
On ne fait donc pas 9 – 4 mais bien 9 – (4 + 1) = 9 – 5 = 4.
Je note donc 4 dans la colonne des dizaines.
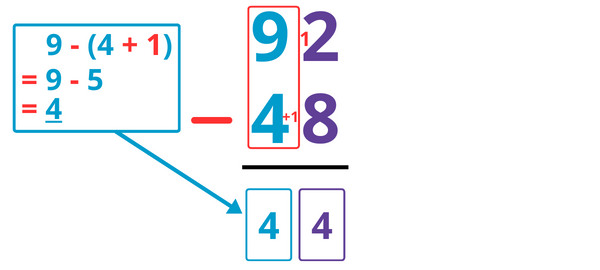
On ne peut toujours pas calculer 2 – 8. On va donc « emprunter » une dizaine à 92.
Je barre le 9 et j’écris 8 à la place, puis j’ajoute une dizaine à côté pour obtenir 12.
12 – 8 = 4, je note donc 4 dans la colonne des unités.
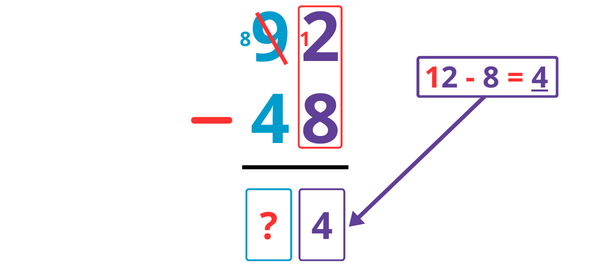
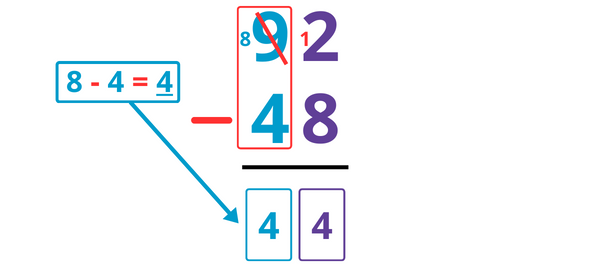
Je soustrais ensuite les dizaines.
8 – 4 = 4.
Je note donc 4 dans la colonne des dizaines.
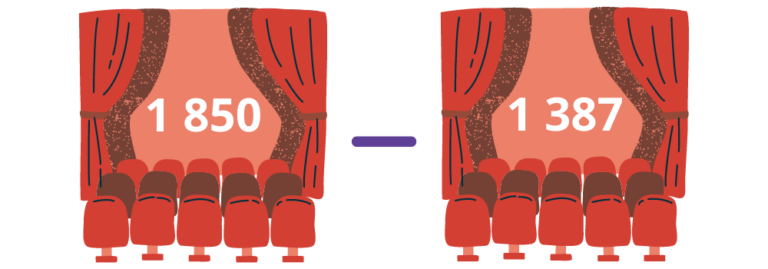
Ici il s’agit d’une soustraction de deux nombres à 4 chiffres. Pour poser la soustraction en colonne, je place les unités sous les unités, les dizaines sous les dizaines, les centaines sous les centaines et les milliers sous les milliers, puis je soustrais les chiffres de chaque colonne.

Je commence par les unités : mais calculer 0 – 7 est impossible !
Avant de soustraire les unités, j’emprunte donc une dizaine que j’ajoute au premier terme dans la colonne des unités (ici le chiffre 0 devient donc 10).
10 – 7 = 3, je note donc 3 dans la colonne des unités.
Mais attention, j’ai emprunté une dizaine, il faut la rendre ! J’ajoute donc +1 au deuxième terme dans la colonne des dizaines (ici j’ajoute donc +1 à côté du chiffre 8).
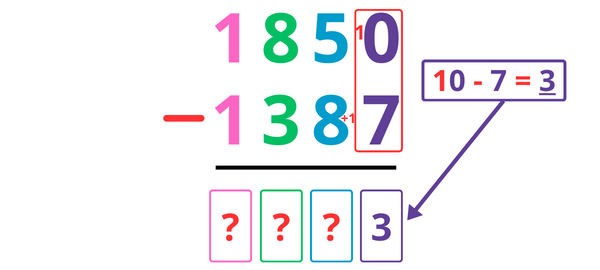
Je soustrais ensuite les dizaines en n’oubliant pas d’ajouter la retenue !
On ne fait donc pas 5 – 8 mais bien 5 – (8 + 1) = 5 – 9.
Calculer 5 – 9 est impossible !
Avant de soustraire les dizaines, j’emprunte donc une centaine que j’ajoute au premier terme dans la colonne des dizaines (ici le chiffre 5 devient donc 15).
15 – 9 = 6, je note donc 6 dans la colonne des dizaines.
Mais attention, j’ai emprunté une centaine, il faut la rendre ! J’ajoute donc +1 au deuxième terme dans la colonne des centaines (ici j’ajoute donc +1 à côté du chiffre 3).
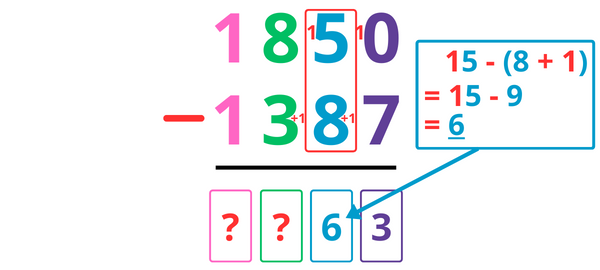
Je soustrais ensuite les centaines en n’oubliant pas d’ajouter la retenue !
On ne fait donc pas 8 – 3 mais bien 8 – (3 + 1) = 8 – 4 = 4.
Je note donc 4 dans la colonne des centaines.
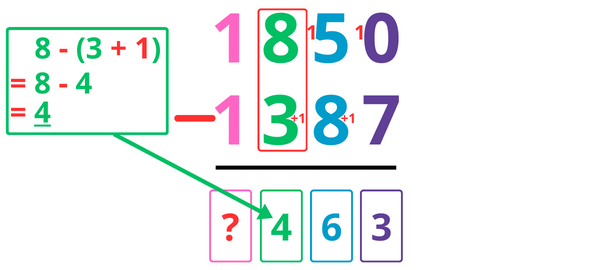
Je soustrais ensuite les milliers.
1 – 1 = 0.
Je note donc 0 dans la colonne des milliers.
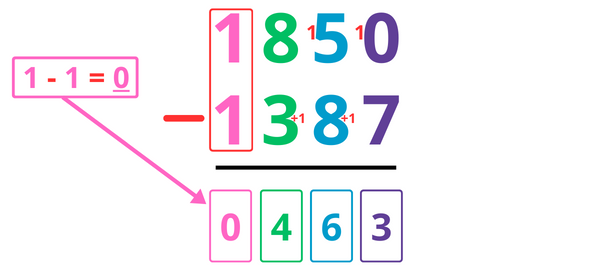
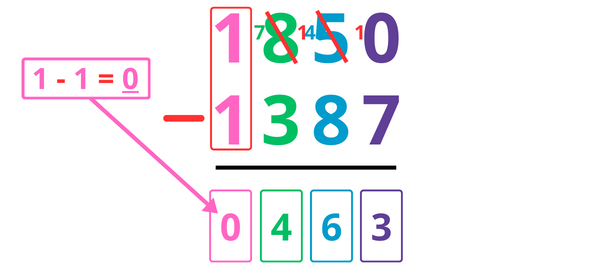
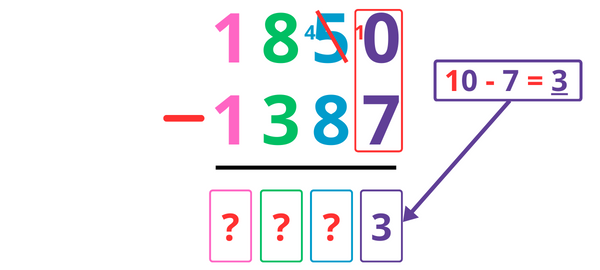
On ne peut pas calculer 0 – 7. On va donc « emprunter » une dizaine.
Je barre le 5 et j’écris 4 à la place (dans la colonne des dizaines), puis j’ajoute une dizaine à côté pour obtenir 10.
10 – 7 = 3, je note donc 3 dans la colonne des unités.
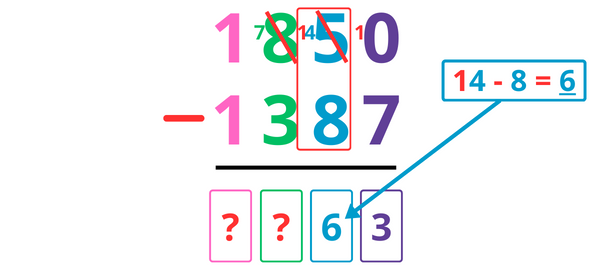
On ne peut pas calculer 4 – 8. On va donc « emprunter » une centaine.
Je barre le 8 et j’écris 7 à la place (dans la colonne des centaines), puis j’ajoute une centaine à côté pour obtenir 14.
14 – 8 = 6, je note donc 6 dans la colonne des dizaines.
7 – 3 = 4, je note donc 4 dans la colonne des centaines.
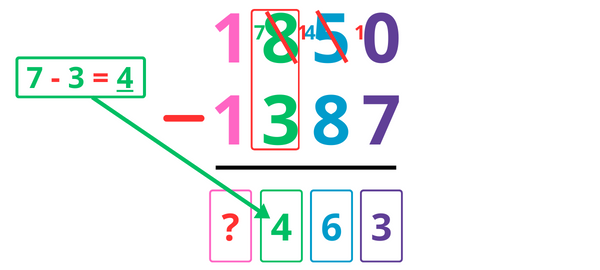
1 – 1 = 0, je note donc 0 dans la colonne des milliers.